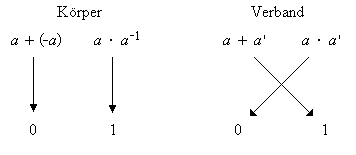Komplement (Verbandstheorie)

Komplementäre Elemente

In einem beschränkten Verband nennt man ein Element ${\displaystyle b}$ ein Komplement von ${\displaystyle a}$, wenn

${\displaystyle a\wedge b=0}$ und ${\displaystyle a\vee b=1}$

gilt.

Ein beschränkter Verband, in dem jedes Element (mindestens) ein Komplement hat, heißt komplementärer Verband.

Im Allgemeinen kann es zu einem Element mehrere komplementäre Elemente geben. Ist das Komplement von ${\displaystyle a}$ eindeutig, dann werden verschiedene Bezeichnungen verwendet: bei Teilmengenverbänden ist ${\displaystyle a^{\complement }}$ üblich, bei Anwendungen in der Logik ${\displaystyle \neg a}$, bei Schaltalgebren ${\displaystyle {\bar {a}}}$.
Es gilt

${\displaystyle \neg 0=1,\neg 1=0}$.

In einem distributiven beschränkten Verband kann jedes Element höchstens ein Komplement haben
Falls ${\displaystyle a}$ ein Komplement ${\displaystyle \neg a}$ hat, dann hat auch ${\displaystyle \neg a}$ ein Komplement, nämlich

${\displaystyle \neg \neg a=a}$.

Ein distributiver komplementärer Verband heißt boolescher Verband oder boolesche Algebra.

Relative Komplemente

Sind ${\displaystyle a,b}$ Elemente eines Verbandes, dann heißt die Menge ${\displaystyle \left\{x\in V\mid a\leq x\land x\leq b\right\}}$ das durch a und b bestimmte Intervall.
Die Definition stimmt auf geordneten Mengen mit der eines abgeschlossenen Intervalls überein und es wird die gleiche Notation ${\displaystyle [a,b]}$ verwendet.

Sind ${\displaystyle c,d\in [a,b]}$, dann heißt ${\displaystyle d}$ relatives Komplement von ${\displaystyle c}$ bezüglich ${\displaystyle [a,b]}$, wenn

${\displaystyle c\wedge d=a}$ und ${\displaystyle c\vee d=b}$ gilt.

Auch hier gilt, dass es in ${\displaystyle [a,b]}$ mehrere zu ${\displaystyle c}$ komplementäre Elemente geben kann und dass aus dem Distributivgesetz die Eindeutigkeit folgt.

Ein Verband heißt relativkomplementär, wenn es in jedem Intervall zu jedem Element ein relatives Komplement gibt.

Ein relativkomplementärer Verband ist ein komplementärer Verband genau dann, wenn er beschränkt ist. Umgekehrt muss ein komplementärer Verband nicht relativkomplementär sein. Jedoch ist ein modularer komplementärer Verband relativkomplementär.

Relative Komplemente können zur Charakterisierung von distributiven Verbänden dienen. Ein Verband ist genau dann distributiv, wenn jedes Element in jedem Intervall höchstens ein relatives Komplement besitzt.

Pseudokomplemente

Sind ${\displaystyle a,b}$ zwei Elemente eines Verbandes, dann nennt man ein größtes Element ${\displaystyle c}$, für das ${\displaystyle a\wedge c\leq b}$ gilt, ein relatives Pseudokomplement von ${\displaystyle a}$ bezüglich ${\displaystyle b}$.

Ein relatives Pseudokomplement von ${\displaystyle a}$ bezüglich ${\displaystyle 0}$ heißt Pseudokomplement von ${\displaystyle a}$.

Ein Verband, in dem für jedes Element ${\displaystyle a}$ ein Pseudokomplement existiert, heißt pseudokomplementärer Verband.

Die Bezeichnung für Pseudokomplemente ist nicht einheitlich.

Eigenschaften

Wenn (relative) Pseudokomplemente existieren, dann sind sie eindeutig bestimmt.

In einem distributiven Verband bildet ${\displaystyle \{x\mid a\wedge x=0\}}$ ein Ideal. Daher ist die Existenz von Pseudokomplementen in endlichen distributivenVerbänden gesichert. Die Distributivität ist wesentlich: ${\displaystyle M_{3}}$ ist nicht pseudokomplementär.

Für Pseudokomplemente muss nicht ${\displaystyle \neg \neg a=a}$ gelten, auch wenn der Verband distributiv ist. Es ist aber immer

${\displaystyle a\leq \neg \neg a}$ und ${\displaystyle \neg \neg \neg a=\neg a}$

Für Pseudokomplemente gilt eins der De Morganschen Gesetzen:

${\displaystyle \neg (a\vee b)=\neg a\wedge \neg b}$

Für die duale Form gilt lediglich:

${\displaystyle \neg a\vee \neg b\leq \neg (a\wedge b)}$

Ein distributiver relativ-komplementärer Verband heißt Heyting-Algebra.

Orthokomplemente

In einem Verband wird eine Funktion ${\displaystyle k\colon V\to V}$ als Orthogonalisierung bezeichnet, wenn sie folgende Bedingungen erfüllt:

• ${\displaystyle a\vee a^{k}=1}$ und ${\displaystyle a\wedge a^{k}=0}$
• ${\displaystyle (a^{k})^{k}=a}$
• ${\displaystyle a\leq b\implies b^{k}\leq a^{k}}$,

Der Verband (mit dieser Abbildung) wird als orthokomplementärer Verband bezeichnet. ${\displaystyle \textstyle a^{k}}$ heißt Orthokomplement von ${\displaystyle a}$ (zu dieser Orthogonalisierung).

Wenn ${\displaystyle V}$ ein distributiver komplementärer Verband ist, dann ist das Komplement von ${\displaystyle a}$ auch sein einzig mögliches Orthokomplement. Im Allgemeinen kann man aber auch in einem distributiven Verband mehrere verschiedene Orthogonalisierungen haben.

Beispiele zu Orthokomplementen

• Ist ${\displaystyle V}$ ein euklidischer Vektorraum und ${\displaystyle U_{1}}$ ein Untervektorraum, dann bilden die zu ${\displaystyle U}$ orthogonalen Vektoren einen Vektorraum ${\displaystyle U_{2}}$ . ${\displaystyle U_{1}}$ und ${\displaystyle U_{2}}$ sind Orthokomplemente im (modularen) Verband der Unterräume von ${\displaystyle V}$.
• Das Beispiel der euklidischen Vektorräume kann zu beliebigen Vektorräumen mit einem inneren Produkt verallgemeinert werden. Verschiedene innere Produkte liefern dabei i. A. verschiedene Orthokomplemente im Verband der Unterräume von ${\displaystyle V}$.

Dies sind typische Beispiele, die auch zur Namensgebung führten.

Literatur

• Gericke Helmuth: Theorie der Verbände. 2. Auflage. BI, Mannheim 1967. 
• Grätzer George: Lattice Theory. First concepts and distributive lattices. W.H.Freeman and Company, 1971, ISBN 978-0-486-47173-0. 

Einzelnachweise