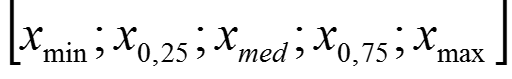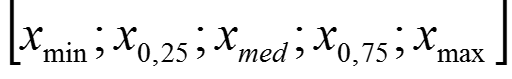Interquartilsabstand (deskriptive Statistik)

Der Interquartilsabstand, auch kurz Quartilsabstand genannt und mit IQA oder IQR (nach der englischen Bezeichnung interquartile range) abgekürzt, ist ein Streuungsmaß in der deskriptiven Statistik. Sortiert man eine Stichprobe der Größe nach, so gibt der Interquartilsabstand an, wie breit das Intervall ist, in dem die mittleren 50 % der Stichprobeelemente liegen.

Definition

Gegeben sei eine Stichprobe ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ mit ${\displaystyle n}$ Elementen, die der Größe nach sortiert sind. Es gilt also ${\displaystyle x_{1}\leq x_{2}\leq \dots \leq x_{n}}$.

Des Weiteren sei ${\displaystyle x_{0{,}25}}$ das untere Quartil und ${\displaystyle x_{0{,}75}}$ das obere Quartil. Diese sind definiert als

${\displaystyle x_{0{,}25}={\begin{cases}{\tfrac {1}{2}}(x_{n\cdot 0{,}25} x_{n\cdot 0{,}25 1}),&{\text{wenn }}n\cdot 0{,}25{\text{ ganzzahlig,}}\\x_{\lfloor n\cdot 0{,}25 1\rfloor },&{\text{wenn }}n\cdot 0{,}25{\text{ nicht ganzzahlig.}}\end{cases}}}$ und ${\displaystyle x_{0{,}75}={\begin{cases}{\tfrac {1}{2}}(x_{n\cdot 0{,}75} x_{n\cdot 0{,}75 1}),&{\text{wenn }}n\cdot 0{,}75{\text{ ganzzahlig,}}\\x_{\lfloor n\cdot 0{,}75 1\rfloor },&{\text{wenn }}n\cdot 0{,}75{\text{ nicht ganzzahlig.}}\end{cases}}}$.

Hierbei bezeichnet ${\displaystyle \lfloor x\rfloor }$ die Abrundungsfunktion. Sie rundet jede Zahl ${\displaystyle x}$ auf die nächste ganze Zahl ab. Es gilt also beispielsweise ${\displaystyle \lfloor 1{,}2\rfloor =1}$ und ${\displaystyle \lfloor 3{,}99\rfloor =3}$.

Der Interquartilsabstand ist dann definiert als

${\displaystyle \operatorname {IQA} =x_{0{,}75}-x_{0{,}25}}$

und ist somit genau die Differenz zwischen dem oberen und dem unteren Quartil.

Beispiel

Betrachte die Stichprobe

${\displaystyle 25;28;4;28;19;3;9;17;29;29}$

mit ${\displaystyle n=10}$ Elementen. Sortiert man die Elemente der Größe nach, so erhält man

${\displaystyle 3;4;9;17;19;25;28;28;29;29}$.

Zur Bestimmung des unteren Quartils berechnet man ${\displaystyle n\cdot 0{,}25=2{,}5}$, was nicht ganzzahlig ist. Daher ist gemäß der oben angegebenen Definition

${\displaystyle x_{0{,}25}=x_{\lfloor n\cdot 0{,}25 1\rfloor }=x_{\lfloor 2{,}5 1\rfloor }=x_{\lfloor 3{,}5\rfloor }=x_{3}=9}$.

Analog folgt

${\displaystyle x_{0{,}75}=x_{\lfloor n\cdot 0{,}75 1\rfloor }=x_{\lfloor 7{,}5 1\rfloor }=x_{\lfloor 8{,}5\rfloor }=x_{8}=28}$.

Damit erhält man für den Interquartilsabstand

${\displaystyle \operatorname {IQA} =x_{0{,}75}-x_{0{,}25}=28-9=19}$.

Aufbauende Begriffe

Aufbauend auf dem Interquartilsabstand wird der mittlere Quartilsabstand definiert, der mit MQA oder QD (nach der englischen Bezeichnung quartile deviation) abgekürzt wird. Er ist definiert als

${\displaystyle \operatorname {MQA} ={\frac {1}{2}}\operatorname {IQA} ={\frac {1}{2}}\left({x_{0{,}75}-x_{0{,}25}}\right)}$.

Im obigen Beispiel wäre der mittlere Quartilsabstand somit

${\displaystyle \operatorname {MQA} ={\frac {1}{2}}\cdot 19=9{,}5}$.

Einzelnachweise